
Spmatrix export dW2_geo using "dW2_geo. * export weight matrix and read it back to compare with above * copy the W2_geo Mata matrix to sp, default is spectral normalization * create custom distance matrix using -geodist. Spmatrix export dW2 using "dW2.txt", replace * export weight matrix and read it back to compare later * copy the W2 Mata matrix to sp, default is spectral normalization * use reciprocal to recover distances and generate new weights You can also remove both normalize(none) options and the results will also match.Ĭode: * create a weight matrix based on geographic distances without normalization * export and compare to the one generated by spmatrix createĬf _all using "dW.dta", allBoth datasets are identical. Spmatrix spfrommata dW2=W id, normalize(none) * import the Mata matrix without normalization * create a distance matrix using -geodist. Spmatrix create idistance dW, replace normalize(none) Spset, modify coordsys(latlong, kilometers) In the following example, I specify that no normalization be done so that you can compare raw inverse distances.Ĭode: * export the distance matrix without normalization You could implement the Haversine formula in Mata but you can also do this in Stata using cross to form all pairwise combinations. Now that you have a way to replicate the distances calculated by Stata's sp* commands, you can repeat what you were trying to do in #1 using great-circle distances. The horizontal axis for each graph is in the units of time that your VAR is estimated in, in this case quarters hence, the impulseresponse graph shows the effect of a shock over a 20-quarter period. geodist lat1 lon1 lat2 lon2, sphere radius(6374.611584000008406) The impulseresponse graph places one impulse in each row and one response variable in each column. * redo with the radius used by spdistance * spdistance uses a different earth radius Great-circle distance (haversine formula, radius of 6371km) = 24.300728 km * redo using geodist (from SSC) using haversine formula (data currently use latitude and longitude) Linked shapefile: NUTS_RG_01M_2013_shp.dta
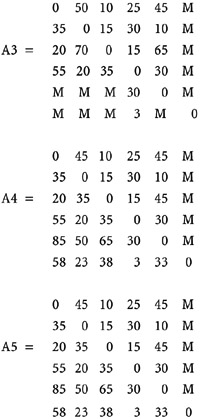
spset, modify coordsys(latlong, kilometers)Ĭoordinates: _CY, _CX (latitude-and-longitude, kilometers) If you may want to have a look at the files, this is the link to the dataset I am using (already spset): I have been struggling all the day, but in fact I obtain different results. Now if everything works, I should observe the same entries in each ij position. Insheet using "dW2.txt", delim(" ") clear Spmatrix export dW2 using dW2.txt, replace
Compute geodist for each row stata manual#
I am using an example that I found into the sp manual (p. Nonetheless, to be sure that I proceed correctly, I firstly try to replicate the inverse distance I have done previously. I generate an inverse distance function using spmatrix idistance.įor some specific reasons, I need to use mata to create my own Matrix. So if your goal is for people to compare your coefficients and levels of significance across models, just presenting the output of esttab with the defaults is sufficient, e.g.I am using Stata 15 to carry out my spatial analysis. Therefore, including the actual p-values in your presentation of the results is not necessary. The sizes of the z-statistics will tell you "how significant" one coefficient is relative to another. Therefore, in the output of esttab, the number of stars is what indicates the level of significance (usually 3 stars for 0.001, 2 stars for 0.01 and 1 star for 0.05, but you can change the defaults). The conventional levels of significance are 0.001, 0.01 and 0.05 (sometimes 0.1). To my point in #7, when presenting the results, most people are interested in whether the coefficient of a variable is significant and not necessarily the actual p-value. So yes, the p-values that you calculate are already displayed in the regression table. In red, we have the coefficients blue, standard errors orange, z-statistics and green the p-values. 46034778 (fraction of variance due to u_i) Group variable: country1 Number of groups = 328 Random-effects GLS regression Number of obs = 9,512 Note: year_29 omitted because of collinearity

xtreg logimport loggdpimp loggdpexp logdist year_*, re 71800838 (fraction of variance due to u_i) Group variable: company Number of groups = 10Ĭorr(u_i, X) = 0 (assumed) Prob > chi2 = 0.0000 Random-effects GLS regression Number of obs = 200


 0 kommentar(er)
0 kommentar(er)
